ALGORITHM
ALGORITHM AND JUSTIFICATION
Depth-First Search Algorithm
DFS algorithm were applied in these pacman game it does not show efficiency and time consuming to arrive at the goal. Furthermore, DFS always checks the right side first before moving on to the other side in order to reach the goal. Imagine that if the goal is located at the shallowest left side, there would be such a long way to go
Breadth-First Search Algorithm
BFS algorithm is better than the DFS algorithm in terms of optimality although it is not the best. To support that, BFS always searches stage-by-stage to check in order to reach the goal
A* Search Algorithm
A* search algorithm is the best in terms of optimality. To support that, it is proven that A* search algorithm did the jobs to minimize the total estimated solution cost especially for these Pac-Man project
DEPTH-FIRST SEARCH ALGORITHM

Figure 1 depicts an example of this DFS algorithm in the project. Red dot represents a ghosts while yellow dot represents the pac-man and each grid will act as the nodes. By using this DFS, from the view of ghost it will always decide to explore east first from its initial state which is from 4 to 7. After it arrives at the new initial state, then it will expand more nodes at the current state if there is an existing node.
Figure 2 illustrates the tile number for the ghost movement by using this DFS algorithm. Based on the figure, the ghost kept moving forward to the east until the end of tiles. This is happening because DFS uses LIFO stack which the last in will be the first out. Although there are paths to the pacman which is the goal, specifically start at tile 21 but it will always choose the frontier of LIFO stack which is tile 13. It will travel all the expanded nodes after it reach the end of the tiles.


DFS algorithm is the modified tree search version where in DFS algorithm it can check again if there are new nodes from the current state. To achieve the goal where pacman is located at node 23, it needs to do looping until z because if there are still more nodes after the looping 5, it will travel those nodes first.
BREADTH-FIRST SEARCH ALGORITHM
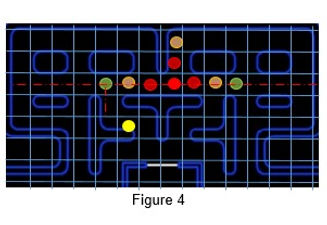
Figure 4 shows the BFS algorithm applied by the ghosts to chase pacman. Firstly, at the initial state which is the root where ghost will expand and there are three predictable paths. In spite of that, from the view of ghost it will always explore the east node for the next initial state. Then when arrived, ghost expand another path if there is one but those expanded paths will be added at the back end of the queue.
Next, the ghost explored the north from the root and found another path. Unfortunately, it will not explore those found paths because the next frontier of the queue is west node from the root.

Figure 5 illustrates the movements by using tiles number. Unlike the DFS algorithm, the simple explanation for the BFS algorithm in exploring paths is stage-by-stage. The first stage is represented by a red ghost where that ghost will travel from tiles number 7 to 5 and 3 while adding the next tile to the FIFO queue. Next, the second stage is represented by the orange ghost and the travels go from tiles 11 to 6 and 2. The looping of this BFS algorithm will continue like that until it reach the goal where the pacman is located.

Figure 6 pictures the flow of the BFS algorithm used by the ghost. It travels stage by stage indicated by a pointer. In addition, every node of each stage will expand and queue it using FIFO list
A* SEARCH ALGORITHM

Figure 7 pictures a scenario by using A* search algorithm. The ghost starts to expand from its root which is 4 as illustrated in Figure 5. Next, it will select the lowest f(n) with h(n) that satisfies certain conditions. The condition that requires this h(n) in these pacman game is the distance to reach the goal which is pacman itself
Figure 8 depicts the movements of ghost to reach pacman. The ghost decides the next movement by using g(n) + h(n). The h(n) values can be referred to based on Figure 9


Figure 9 indicates movements of ghost to catch pacman in graph form. Ghost will always choose the least of h(n) in order to reach its destination. Moreover, the g(n) is always the actual cost to the destination